komputer "dari awal sampai sekarang"

Sejarah Komputer - Komputer adalah sebuah perangkat yang saat ini banyak digunakan dalam kehidupan sehari-hari. Adanya komputer sebagai penunjang aktifitas manusia, dapat mempermudah setiap pekerjaan yang dilakukan.

Hal tersebut terbukti dengan digunakannya komputer, dalam setiap lini kehidupan di zaman yang modern ini. Tidak bisa dipungkiri lagi, bahwa manusia saat ini cenderung bergantung pada komputer dalam kesehariannya.

Sebagai contoh, saat ini fungsi komputer untuk mengetik sebuah surat menjadi lebih efisien, dibandingkan menulis surat dengan tangan. Jika salah pengetikan pada komputer, maka kita bisa langsung menghapus dan merevisinya. Tapi ketika menulis surat dengan tangan di atas selembar kertas, jika terjadi kesalahan maka kita harus menulisnya dari awal, apa bila menulisnya menggunakan pulpen.

Sejarah Komputer Lengkap

Pada dasarnya arti komputer itu cukup luas, tidak hanya sekedar perangkat mesin berteknologi tinggi, dengan sekumpulan chip dan kabel di dalamnya. Tapi komputer adalah alat yang digunakan untuk mengolah data, menurut perintah yang telah dirumuskan sebelumnya.

Jenis-jenis komputer juga cukup banyak, tidak hanya laptop dan komputer desktop yang setiap hari kita lihat saja. Tapi juga mencakup semua perangkat elektronik, yang bisa digunakan untuk mengolah data, berdasarkan perintah yang sudah ditentukan oleh operator.

Sejarah komputer dari generasi ke generasi, memang sudah banyak mengalami perubahan. Bahkan para ilmuan sudah banyak yang menemukan berbagai macam fungsi baru dari komputer itu sendiri. Sehingga pada era teknologi yang pesat seperti sekarang ini, fungsi komputer sudah bisa dirasakan di berbagai lini kehidupan.

Sejarah komputer sendiri terbagi menjadi lima generasi. Masing-masing generasi komputer akan dijelaskan secara lengkap pada pembahasan berikut ini.

Komputer Generasi Pertama (1946 - 1959) Tabung Vakum

Pada tahun 1946 komputer generasi pertama dibuat menggunakan tabung vakum, yang menjadi komponen dasar pembuatannya. Tabung vakum yang menjadi komponen dasar ini, dikenal tidak efisien dalam beberapa aspek. Karena komponen ini akan lebih cepat panas ketika digunakan, dan membutuhkan daya listrik yang besar untuk mengoperasikannya.

Salah satu contoh komputer generasi pertama adalah ENIAC (Electronic Numerical Integrator and Computer). Perangkat komputer generasi pertama ini dibuat oleh J. Presper Eckert dan John Mauchly di University of Pennsylvania. Keduanya membangun ENIAC dengan menggunakan 18.000 tabung vakum berukuran 1800 kaki, dan memiliki berat mencapai 30 ton.

Bahasa yang digunakan pada kompter generasi pertama ini adalah bahasa mesin. Bahasa ini menjadi bahasa pemrograman yang paling dasar, dan bahasa pemrograman ini hanya bisa dimengerti oleh komputer. Biaya yang dibutuhkan untuk membuat perangkat komputer ini mencapai 1 juta dollar. Tapi sayangnya kemampuan komputer generasi ini masih sangat terbatas, untuk dapat memecahkan suatu masalah dalam satu waktu.

Operator harus menggunakan kartu berlubang (punched cards), dan pita kertas untuk melakukan input. Sedangkan otuput yang dihasilkan berupa sebuah print out. Dengan biaya pembuatan yang cukup fantastis, sangat disayangkan fungsi komputer generasi pertama ini belum maksimal.

Komputer Generasi Kedua (1959 - 1965) Transistor

Pada tahun 1959 teknologi transistor dimanfaatkan sebagai komponen pembuatan komputer. Peran tabung vakum pada komputer generasi pertama, digantikan dengan hadirnya teknologi transistor. Karena komponen ini dinilai lebih efisien dibanding tabung vakum. 

Komputer dengan komponen dasar transitor, memiliki ukuran yang lebih kecil dibanding tabung vakum, dan daya listrik yang dibutuhkan untuk mengoperasikannya lebih kecil. Biaya pembuatan komputer generasi kedua ini juga lebih murah, dibandingkan dengan komputer generasi pertama yang menggunakan tabung vakum.

Bahasa pemrograman pada komputer generasi ini juga sudah mulai dikembangkan. Bahasa mesin yang digunakan sebelumnya, kemudian digantikan dengan bahasa Assembly atau bahasa simbolik. Dengan bahasa pemrograman ini, maka programer bisa memberikan instruksi mengguanakan kata-kata.

Komputer Generasi Ketiga (1965 - 1971) Integrated Circuit

Generasi Komputer ketiga diawali pada tahun 1965, pada masa itu komputer dibuat menggunakan Integrated Circuit (ICs). Teknologi sirkuit terintegrasi ini, menggeser peran transistor sebagai komponen dasar komputer pada masa itu. Tapi transistor masih tetap digunakan, hanya saja ukurannya sudah diperkecil. Beberapa transistor berukuran kecil tersebut, diletakan pada sebuah IC, bersama dengan resistor dan juga kapasitor.

Jack Kilby adalah seorang insinyur listrik, yang berhasil mengembangkan IC pertama kali. Dari penemuannya itu, Jack Kilby diberikan hadiah nobel. Karena temuannya tersebut, berhasil meningkatkan kecepatan dan efisiensi komputer secara signifikan. Integrated Circuit ini juga berhasil membuat ukuran komputer menjadi lebih kecil dari sebelumnya.

Komputer generasi ketiga menjadi komputer pertama, yang memungkinkan operator berinteraksi dengan menggunakan keyborad, serta monitor dengan tampilan sistem operasi di dalamnya. Selain itu, komputer pada generasi ini menghabiskan biaya pembuatan yang lebih murah, sehingga bisa dijangkau oleh masyarakat umum.

Komputer Generasi Keempat (1971 - Sekarang) Microprosesor

Komputer yang kita gunakan saat ini, merupkan komputer generasi keempat. Dimana pada komputer generasi ini, dibuat dengan komponen dasar yang disebut Microprosesor. Di dalam sebuah chip Microprosesor, terdapat ribuan transistor dan beberapa macam elemen sirkuit lainnya, yang terhubung menjadi satu.

Intel menjadi perusahaan yang paling berpengaruh, dalam perkembangan chip Microprosesor. Karena mereka berhasil menciptakan Intel 4004 chip, yang menjadi langkah awal perkembangan komputer pada tahun-tahun berikutnya. Perusahaan Intel berhasil menggantikan komponen komputer berkuran besar, yang kini menjadi sangat kecil dan lebih efisien.

Pada tahun 1971 IBM menciptakan komputer, yang didesain secara khusus untuk kalangan rumahan. Sedangkan Apple memperkenalkan Macinthos pertama kali pada tahun 1984, sebagai sebuah sistem operasi untuk mengoperasikan perangkat komputer.

Perkembangan komputer terus berlajut pada tahun-tahun berikutnya, sehingga lahirlah ide untuk membuat jaringan komputer, yang kemudian mengarah pada ditemukannya internet. Banyak kemajuan besar yang terjadi pada komputer generasi kelima, seperti diciptakannya Mouse, Graphical User Interface (GUI), hingga komputer jinjing atau laptop.

Komputer Generasi Kelima (Sekarang - Masa Depan) Artificial intelligence

Komputer generasi kelima ini sebenarnya masih dalam tahap pengembangan. Komputer generasi ini akan memiliki teknologi, yang dibuat berdasarkan kecerdasan buatan (Artificial intelligence).

Pengembangan komputer generasi ini, bertujuan untuk menghasilkan sebuah perangkat komputer yang dapat merespon, apa yang diinput menggunakan bahasa yang digunakan manusia. Selain itu, komputer generasi ini juga diharapkan bisa mempelajari lingkungan disekitarnya, serta dapat menyesuaikan dirinya sendiri.

Komputer kuantum, nanoteknologi dan molekuler menjadi kunci utama, untuk mengembangkan komputer generasi kelima ini. Sehingga komputer ini bisa memiliki keceradasan buatan, yang setara dengan kecerdasan manusia.

ENIAC => Electronic Numerical Integrator and Calculator (ENIAC) merupakan generasi pertama komputer digital elektronik yang digunakan untuk kebutuhan umum. Pgamroposal ENIAC dirancang oada tahun 1942, dan mulai dibuat pada tahun 1943 oleh Dr. John W. Mauchly dan John Presper Eckert di Moore School of Electrical Engineering (University of Pennsylvania) dan baru selesai pada tahun 1946. ENIAC berukuran sangat besar, untuk penempatannya membutuhkan ruang 500m2. ENIAC menggunakan 18.000 tabung hampa udara, 75.000 relay dan saklar, 10.000 kapasitor, dan 70.000 resistor. Ketika dioperasikan, ENIAC membutuhkan daya listrik sebesar 140 kilowatt dengan berat lebih dari 30 ton, dan menempati ruangan 167 m2.Mesin Von Neumann => Mesin ini dikembangkan oleh seorang ahli matamatika yaitu John Von Neumann yang juga merupakan kosultan proyek ENIAC. Mesin ini dikembangkan mulai tahun 1945 yang memberikan gagasan sebagai stored-program concept, yaitu sebuah konsep untuk mempermudah proses program agar dapat direpresentasikan dalam bentuk yang cocok untuk penyimpanan dalam memori untuk semua data. Gagasan ini juga dibuat hampir pada waktu yang bersamaan dengan Turing. Selanjutnya Von Neumann mempublikasikannya dengan nama baru yaitu: Electronic Discrete Variable Computer (EDVAC). Semua input dan output dilakukan melalui kartu plong. Dalam waktu satu detik, ENIAC mampu melakukan 5.000 perhitungan dengan 10 digit angka yang bila dilakukan secara manual oleh manusia akan memakan waktu 300 hari, dan ini merupakan operasi tercepat saat itu dibanding semua komputer mekanis lainnya. ENIAC dioperasikan sampai tahun 1955. Teknologi yang digunakan ENIAC adalah menggunakan tabung vakum yang dipakai oleh Laboratorium Riset Peluru Kendali Angkatan Darat (Army’s Ballistics Research Laboratory-LBR) Amerika Serikat.

Selanjutnya mesin ini dikembangkan kembali dengan perbaikan-perbaikan pada tahun 1947, yang disebut sebagai generasi pertama komputer elektronik terprogram modern yang disediakan secara komersial dengan nama EDVAC, EDSAC (Electronic Delay Storage Automatic Calculator), dan UNIVAC1 dan 2 (Universal Automatic Computer) yang dikembangkan oleh Eckert dan Mauchly. Untuk pertama kalinya komputer tersebut menggunakan Random Access Memory (RAM) untuk menyimpan bagian-bagian dari data yang diperlukan secara cepat. Dengan konsep itulah John Von Neumann dijuluki sebagai bapak komputer modern pertama di dunia yang konsepnya masih digunakan sampai sekarang. John Von Neumann lahir di Budapest, Hongaria 28 Desember 1903 dan meninggal pada tanggal 8 Februari 1957 di Washington DC, AS. Von Neumann sangat cerdas dalam matematika dan angka-angka. Pada usia eman tahun dia sudah dapat menghitung pembagian angka dengan delapan digit tanpa menggunakan kertas atau alat bantu lainnya. Pendidikannya dimulai di University of Budapest pada tahun 1921 di jurusan kimia. Tapi kemudian dia kembali kepada kesukaannya, matematika, dan menyelesaikan doktoralnya di bidang matematika di tahun 1928. di tahun 1930 dia mendapatakan kesempatan pergi ke Princeton University (AS). Pada tahun 1933, Institute of Advanced Studies dibentuk dan dia menjadi salah satu dari enam professor matematika di sana. Von Neumann kemudian menjadi warga negara Amerika.

Von Neumann juga merupakan orang pertama yang mencetuskan istilah “Game Theory” yang kemudian berkembang menjadi ilmu tersendiri. Game theory bermanfaat untuk mensimulasikan permainan, seperti catur, bridge, dan sejenisnya. Dia juga bermanfaat untuk mensimulasikan perang.komputer Komersial Pertama => Pada pertengahan tahun 1950 UNIVAC mengalami kemajuan dalam beberapa aspek pemrograman tingkat lanjut, sehingga merupakan komputer general purpose pertama yang didesain untuk menggunakan angka dan huruf dan menggunakan pita magnetik sebagai media input dan output-nya. Inilah yang dikatakan sebagai kelahiran industri komputer yang didominasi oleh perusahaan IBM dan Sperry. Komputer UNIVAC pertama kali digunakan untuk keperluan kalkulasi sensus di AS pada tahun 1951, dan dioperasikan sampai tahun 1963.Komputer-Komputer IBM => IBM memproduksi IBM 605 dan IBM 701 pada tahun 1953 yang berorientasi pada aplikasi bisnis dan merupakan komputer paling populer sampai tahun 1959. IBM 705 dikeluarkan untuk menggantikan IBM 701 yang kemudian memantapkan IBM dalam industri pengolahan data.Komputer Generasi II (1959-1964) =>Komputer generasi kedua ditandai dengan ciri-ciri sebagai berikut:* Menggunakan teknologi sirkuit berupa transistor dan diode untuk menggantikan tabung vakum.* Sudah menggunakan operasi bahasa pemrograman tingkat tinggi seperti FORTRAN dan COBOL.* Kapasitas memori utama dikembangkan dari Magnetic Core Storage.* Menggunakan simpanan luar berupa Magnetic Tape dan Magnetic Disk.* Kemampuan melakukan proses real time dan real-sharing.* Ukuran fisiknya sudah lebih kecil dibanding komputer generasi pertama.* Proses operasi sudah lebih cepat, yaitu jutaan operasi perdetik.* Kebutuhan daya listrik lebih kecil.* Orientasi program tidah hanya tertuju pada aplikasi bisnis, tetapi juga aplikasi teknik.

UNIVAC III

Dibanding denga tabung, teknologi transistor jauh lebih efisien sebagai switch dan dapat diperkecil ke skala mikroskopik. Pada tahun 2001 peniliti Intel telah memperkenalkan silikon paling kecil dan paling cepat di dunia, dengan ukuran 20 nanometer ata sebanding dengan sepermiliar meter, yang akan digunakan pada prosesor dengan kecepatan 20 GHz (Giga Hertz). Era ini juga menandakan permulaan munculnya minikomputer yang merupakan terbesar kedua dalam keluarga komputer. Harganya lebih murah dibanding dengan generasi pertama. Komputer DEC PDP-8 adalah minikomputer pertama yang dibuat tahun 1964 untuk pengolahan data komersial.

Jenis-jenis komputer lain yang muncul pada generasi ini diantaranta UNIVAC III, UNIVAC SS80, SS90, dan 1107, IBM 7070, 7080, 1400, dan 1600.

Komputer Generasi III (1964-1970)

Pada generasi ketiga inilah teknologi Integrated Circuit (IC) menjadi ciri utama karena mulai digunakan pada sebuah perangkat komputer hingga generasi sekarang. Komponen IC berbentuk hybrid atau solid (SLT) dan monolithyc (MST). SLT adalah transistor dan diode diletakkan terpisah dalam satu tempat sedangkan MST adalah elemen transistor, diode, dan resistor diletakkan bersama dalam satu chip. MST lebih kesil tetapi mempunyai kemmapuan lebih besar dibanding SLT.

IC dibuat pertama kali oleh Texas Istruments dan Fairchild Semiconductor pada tahun 1959 yang hanya berisi enam transistor. Bisa kita bandingkan bahwa prosesor saat ini yang kita gunakan telah memiliki jutaan, puluhan, ratusan juta transistor, bahkan telah didesain prosesor dengan miliaran transistor. Sebuah perkembangan yang luar biasa dalam masa kurang dari setengah abad.

Ciri-ciri komputer generasi ketiga adalah:

* Karena menggunakan IC maka kinerja komputer menjadi lebih cepat dan tepat. Kecepatannya hampir 10.000 kali lebih cepat dari komputer generasi pertama.* Peningkatan dari sisi software.* Kapasitas memori lebih besar, dan dapat menyimpan ratusan ribu karakter (sebelumnya hanya puluhan ribu).* Menggunakan media penyimpanan luar disket magnetik (external disk) yang sifat pengaksesan datanya secara acak (random access) dengan kapasitas besar (jutaan karakter).* Penggunaan listrik lebih hemat.* Kemampuan melakukan multiprocessing dan multitasking.* Telah menggunakan terminal visual display dan dapat mengeluarkan suara.* Harganya semakin murah.* Kemampuan melakukan komunikasi dengan komputer lain.

IBM S/360, UNIVAC 1108, UNIVAC 9000, Burroughts 5700, 6700, 7700, NCR Century, GE 600, CDC 3000, 6000, dan 7000, PDP-8, dan PDP-11 (pabrik pembuatnya adalah Digital Equipment Corporation) merupakan contoh-contoh komputer generasi ketiga.

Komputer Generasi IV (1970-1980-an)

Komputer generasi keempat merupakan kelanjutan dari generasi III. Bedanya bahwa IC pada generasi IV lebih kompleks dan terintegrasi. Sejak tahun 1970 ada dua perkembangan yang dianggap sebagai komputer generasi IV. Pertama, penggunaan Large Scale Integration (LSI) yang disebut juga dengan nama Bipolar Large Large Scale Integration. LSI merupakan pemadatan beribu-ribu IC yang dijadikan satu dalam sebuah keping IC yang disebut chip. Istilah chip digunakan untuk menunjukkan suatu lempengan persegi empat yang memuat rangkaian terpadu IC. LSI kemudian dikembangkan menjadi Very Large Scale Integration (VLSI) yang dapat menampung puluhan ribu hingga ratusan ribu IC. Selanjutnya dikembangkannya komputer mikro yang menggunakan mikroprosesor dan semikonduktor yang berbentuk chip untuk memori komputer internal sementara generasi sebelumnya menggunakan magnetic core storage.Komputer Generasi IV: Apple II

Komputer Generasi IV: Apple II

Perusahaan Intel pada tahun 1971 memperkenalkan mikrokomputer 4 bit yang menggunakan chip prosesor dengan nama 4004 yang berisi 230 transistor dan berjalan pada 108 KHz (Kilo-Hertz) dan dapat mengeksekusi 60.000 operasi per detik. Dilanjutkan pada tahun 1972, Intel memperkenalkan mikrokomputer 8008 yang memproses 8 bit informasi pada satu waktu. Selanjutnya mikroprosesor 8080 dibuat pada tahun 1974, dan merupakan prosesor untuk tujuan umum pertama. Sebelumnya prosesor 4004 dan 8008 dirancang untuk kebutuhan aplikasi tertentu, dan prosesor 8080 memiliki kemampuan lebih cepat dan memilki set instruksi yang lebih kaya, serta memiliki kemampuan pengalamatan yang lebih besar. Pada generasi keempat ini tampilan monitor masih satu warna (green color).

Komputer Generasi IV: PDP 11

Komputer-komputer generasi keempat diantaranya adalah IBM 370, Apple I dan Apple II, PDP-11, VisiCalc, dan Altair yang menggunakan prosesor Intel 8080, dengan sistem operasi CP/M (Control Program for Microprocessor), dengan bahasa pemrograman Microsoft Basic (Beginners Allpurpose Symbolic Instruction Code). Sebagai catatan bahwa pada komputer-komputer generasi keempat ini tidak satupun yang PC-Compatible atau Macintosh-Compatible. Sehingga pada generasi ini belum ditentukan standar sebuah komputer terutama personal computer (PC).

Komputer Generasi V (1980-an-sekarang)

Akhir tahun 1980, IBM memutuskan untuk membangun sebuah komputer personal (PC) secara massal, yang pada tanggal 12 Agustus 1981 menjadi sebuah standar komputer PC, dan pada akhirnya hingga saat ini PC dikenal dengan nama standar IBM-PC. Prosesor yang digunakan adalah 8088/8086 yang menjadi standar komputer saat ini, menggunakan basis proses 16 bit persatuan waktu. Dengan lahirnya komputer generasi kelima ini, IBM bekerja sama dengan Microsoft untuk mengembangkan software di dalamnya. Hingga saat ini Microsoft mendominasi kebutuhan software di dunia PC.

Pada perkembangan selanjutnya perubahan besar terjadi bahwa sejak IBM-PC diperkenalkan dan bukan menjadi satu-satunya manufaktur PC-compatible, maka standar baru dalam dunia industri PC lebih dikembangkan oleh perusahaan lain seperti Intel dan Microsoft yang dipelopori oleh W. Bill Gates yang menjadi pionir standar hardware dan software dunia.

Pada generasi kelima ini, telah dilakukan pengembangan dengan apa yang dinamakan Josephson Junction, teknologi yang akan menggantikan chip yang mempunyai kemampuan memproses trilyunan operasi perdetik sementara teknologi chip hanya mampu memproses miliaran operasi perdetik. Komputer pada generasi ini akan dapat menerjemahkan bahasa manusia, manusia dapat langsung bercakap-cakap dengan komputer serta adanya penghematan energi komputer. Sifat luar biasa ini disebut sebagai “Artificial Intelligence”, selain itu juga berbasis Graphic User Interface (GUI), multimedia, dan multikomunikasi.

Contoh-contoh komputer yang lahir pada generasi kelima berbasis x86, seperti chip 286 yang diperkenalkan pada tahun 1982 dengan 134.000 transistor, kemudian chip 386 pada tahun 1983 dengan 275.000 transistor, sedangkan chip 486 diperkenalkan tahun 1989 yang memiliki 1,2 juta transistor. Selanjutnya pada tahun 1993 Intel memperkenalkan keluarga prosesor 586 yang disebut Pentium 1 dengan jumlah transistor 3,1 juta untuk melakkan 90 MIPS (Million Instruction Per Second). Kemudian dilanjutkan pada generasi berikutnya yaitu Pentium 2, 3, dan 4.

Pada akhir tahun 2000 Intel memperkenalkan Pentium 4, yang merupakan prosesor terakhir dalam keluarga Intel dengan arsitektur 32 bit (IA-32). Tahun 2001 Intel mengumumkan prosesor Itanium yang merupakan prosesor dengan basis arsitektur 64 bit (IA-64) pertama. Itanium merupakan prosesor pertama milik Intel dengan instruksi-instruksi 64 bit dan akan menelurkan satu generasi baru dari sistem operasi dan aplikasi, sementara masih mempertahankan backward compatibility dengan software 32 bit. Perlu diketahui bahwa sejak dikeluarkannya prosesor 386, komputer beroperasi pada 32 bit per satuan waktu dalam mengeksekusi informasi hingga Pentium 4. Hingga sekarang komputer yang digunakan kebanyakan masih yang berbasis 32 bit.Pada generasi pentium, selain ciri khas pada peningkatan kecepatan akses datanya juga tampilan gambar sudah beresolusi (kualitas gambar) bagus dan berwarna serta multimedia, dan yang lebih penting adalah fungsi komputer menjadi lebih cerdas. Meskipun komputer pada generasi ini ukuran fisiknya menjadi lebih kecil dan sederhana namun memiliki kemampuan yang semakin canggih.

Sistem Bilangan pada Elektronika Digital

Dickson Kho Teori Elektronika

Sistem Bilangan pada Elektronika Digital
Sistem Bilangan pada Elektronika Digital – Bilangan adalah objek matematika yang digunakan untuk pengukuran, penghitungan dan pelabelan. Sedangkan yang dimaksud dengan Sistem Bilangan adalah sistem penulisan yang digunakan untuk mengekspresikan bilangan. Sistem Bilangan juga dapat didefinisikan sebagai cara yang digunakan untuk mewakili besaran suatu item fisik. Setiap sistem bilangan menggunakan bilangan dasar atau basis tertentu yang dalam bahasa Inggris biasanya disebut dengan “Base” atau “Radix”. Dalam pengertiannya, Base atau Radix dari sistem bilangan adalah jumlah total digit atau jumlah suku angka yang digunakan dalam suatu sistem bilangan. Contohnya pada sistem bilangan Desimal, Radix dari sistem bilangan Desimal adalah 10, yang artinya adalah memiliki 10 suku angka yakni 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Sistem Bilangan pada Elektronika Digital
Dalam dunia Elektronika Digital, Pengetahuan Sistem Bilangan merupakan pengetahuan dasar yang wajib dipelajari, karena semua rangkaian digital yang dirancang ataupun perangkat digital menggunakan konsep sistem bilangan tersebut. Sistem Bilangan dalam elektronika digital digunakan untuk mewakili informasi yang akan diolah ataupun pemrosesan hingga hasil olahannya. Sistem Bilangan yang umumnya digunakan dalam teknik elektronika digital diantaranya adalah Sistem Bilangan Desimal, Biner, Heksadesimal dan Oktal.

Sistem Bilangan Desimal (Decimal)
Basis atau Radix dari sistem bilangan Desimal ini adalah 10 yaitu berkisar dari angka 0 hingga 9 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Digit atau angka yang terletak di sebelah kiri koma desimal disebut dengan bilangan bulat sedangkan digit atau angka yang terletak di sebelah kanan titik desimal disebut dengan bilangan pecahan. Sistem Bilangan Desimal ini merupakan sistem bilangan yang dipergunakan pada kehidupan kita sehari-hari. Perlu diketahui bahwa Indonesia menggunakan koma untuk menunjukan separator (pemisah) antara bilangan bulat dengan bilangan pecahan sedangkan negara-negara lainnya menggunakan tanda titik sebagai separator pecahannya.

Di sistem bilangan desimal ini, digit atau angka yang berada di posisi berturut-turut disebelah kiri koma desimal memiliki bobot 100, 101, 102, 103, 104 dan seterusnya. Sedangkan digit atau angka yang berada di posisi berturut-turut disebelah kanan koma desimal memiliki bobot 10-1, 10-2, 10-3, 10-4 dan seterusnya. Artinya, setiap posisi digit yang ditempati memiliki bobot masing-masing dengan pangkat bilangan yang berbasis 10.

Contoh :

Kita ambil contoh pada sebuah bilangan Desimal 235,12. Bagian bilangan bulatnya adalah 235 sedangkan bagian bilangan pecahannya adalah 0,12. Digit-digitnya 5, 3, dan 2 masing-masing memiliki bobot 102, 101 dan 100. Demikian juga digit 1 dan 2 dibelakang koma memiliki bobotnya masing-masing yaitu 10-1 dan 10-2.

Secara Matematis, dapat kita tulis sebagai berikut :

235,12 = (2 x 102) + (3 x 101) + (5 + 100) + (1 x 10-1) + (2 x 10-2)

Sistem Bilangan Biner (Binary)
Sistem Bilangan Biner atau Binary Numbering System adalah sistem bilangan yang berbasis dua dan merupakan sistem bilangan yang digunakan oleh semua rangkaian elektronika yang bersistem digital. Basis atau Radix dari sistem bilangan Biner ini adalah 2 yaitu angka 0 dan 1 saja. Di sistem bilangan Biner ini, setiap angka atau digit memiliki bobot 20, 21, 22, 23, 24 dan seterusnya.
Baca juga : Pengertian Aljabar Boolean dan Hukum Aljabar Boolean.

Contoh :

Sebagai contoh, kita gunakan bilangan Biner 10112. Ini berarti digit-digitnya yaitu 1, 0, 1 dan 1 memiliki bobot masing-masing 23, 22, 21 dan 20 (dihitung dari kanan ke kiri).

Secara Matematis, dapat kita tulis sebagai berikut :

10112 = (1 x 23) + (0 x 22) + (1 + 21) + (1 x 20)

Jika kita konversikan bilangan biner 10112 ke bilangan desimal akan menjadi 11.

Baca juga : Cara Konversi Bilangan Desimal ke Bilangan Biner.

Sistem Bilangan Oktal (Octal)
Sistem Bilangan Oktal atau Octal Numbering system adalah sistem bilangan yang berbasis delapan (8). Jadi, angka yang digunakan adalah berkisar diantara 0 hingga 7 (0, 1, 2, 3, 4, 5, 6, 7). Di sistem bilangan Oktal ini, masing-masing angka atau digit memiliki bobot 80, 81, 82, 83, 84 dan seterusnya.

Contoh :

Sebagai contoh, kita gunakan bilangan Oktal 72148. Ini berarti digit-digitnya yaitu 7, 2, 1 dan 4 memiliki bobot masing-masing 83, 82, 81 dan 80.

Secara Matematis, dapat kita tulis sebagai berikut :

72148 = (7 x 83) + (2 x 82) + (1 + 81) + (4 x 80)

Jika kita konversikan bilangan Oktal 72148 bilangan Desimal akan menjadi 3724.

Baca juga : Cara Konversi Bilangan Desimal ke Bilangan Oktal.

Sistem Bilangan Heksadesimal (Hexadecimal)
Sistem Bilangan Heksadesimal atau Hexadecimal Numbering System adalah sistem bilangan yang berbasis 16. Sistem Bilangan Heksadesimal ini menggunakan angka atau digit 0 hingga 9 dan huruf A sampai F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Huruf A hingga F ekivalen dengan 10 hingga 16. Jadi, pada dasarnya sistem bilangan Heksadesimal ini merupakan gabungan angka dan huruf. Di sistem bilangan Heksadesimal ini, masing-masing angka atau digit memiliki bobot 160, 161, 162, 163, 164 dan seterusnya.

Contoh :

Sebagai contoh, kita gunakan bilangan Oktal 7A1C16. Ini berarti digit-digitnya yaitu 7, A, 1 dan C memiliki bobot masing-masing 163, 162, 161 dan 160.

Secara Matematis, dapat kita tulis sebagai berikut :

7A1C16 = (7 x 163) + (10 x 162) + (1 + 161) + (2 x 160)

Jika kita konversikan bilangan Heksadesimal 7A1C16 ke bilangan Desimal akan menjadi 31260

Tabel 1. Nilai Bilangan Desimal dan Biner

Kolom desimal

Kolom biner

C

102 = 100

(ratusan)

B

101 = 10

(puluhan)

A

100 = 1

(satuan)

C

22 = 4

(empatan)

B

21 = 2

(duaan)

A

20 = 1

(satuan)

Setiap digit biner disebut bit; bit paling kanan disebut least significant bit (LSB), dan bit paling kiri disebut most significant bit (MSB).

Tabel 2. Daftar Bilangan Desimal dan Bilangan Biner Ekivalensinya

Desimal

Biner

C (MSB)

(4)

B

(2)

A (LSB)

(1)

0

1

2

3

4

5

6

7

0

0

0

0

1

1

1

1

0

0

1

1

0

0

1

1

0

1

0

1

0

1

0

1

B. Bilangan Oktal
Bilangan Oktal adalah sistem bilangan yang berbasis 8 dan mempunyai delapan simbol bilangan yang berbeda : 0,1,2,….,7.

Teknik pembagian yang berurutan dapat digunakan untuk mengubah bilangan desimal menjadi bilangan oktal. Bilangan desimal yang akan diubah secara berturut-turut dibagi dengan 8 dan sisa pembagiannya harus selalu dicatat. Sebagai contoh, untuk mengubah bilangan 581910 ke oktal, langkah-langkahnya adalah :

5819/8  =   727,       sisa 3, LSB

727/8    =   90,         sisa 7

90/8       =   11,         sisa 2

11/8       =   1,           sisa 3

1/8         =   0,           sisa 1, MSB

Sehingga 581910 = 132738

· Bilangan Oktal dan Biner

Setiap digit pada bilangan oktal dapat disajikan dengan 3 digit bilangan biner, lihat Tabel 1.5. Untuk mengubah bilangan oktal ke bilangan biner, setiap digit oktal diubah secara terpisah. Sebagai contoh, 35278 akan diubah sebagai berikut:

38 = 0112, MSB

58 = 1012

28 = 0102

78 = 1112, LSB

Sehingga bilangan oktal 3527 sama dengan bilangan 011 101 010 111.

Sebaliknya, pengubahan dari bilangan biner ke bilangan oktal dilakukan dengan mengelompokkan setiap tiga digit biner dimulai dari digit paling kanan, LSB. Kemudian, setiap kelompok diubah secara terpisah ke dalam bilangan oktal. Sebagai contoh, bilangan 111100110012 akan dikelompokkan menjadi 11 110 011 001, sehingga.

112    =   38, MSB

1102      =        68

0112 =   38

0012 =   18­, LSB

Jadi, bilangan biner 11110011001 apabila diubah menjadi bilangan oktal akan diperoleh 36318.

C. Bilangan Hexdadesimal
Bilangan heksadesimal, sering disingkat dengan hex, adalah bilangan dengan basis 1610, dan mempunyai 16 simbol yang berbeda, yaitu 0 sampai dengan 15.

Bilangan yang lebih besar dari 1510 memerlukan lebih dari satu digit hex. Kolom heksadesimal menunjukkan eksponen dengan basis 16, yaitu 160 = 1, 161 = 16, 162 = 256, dan seterusnya. Sebagai contoh :

152B16  =   (1 x 163) + (5 x 162) + (2 x 161) + (11 x 160)

              =   1 x 4096 + 5 x 256 + 2 x 16 + 11 x 1

              =   4096 + 1280 + 32 + 11

              =   541910

Sebaliknya, untuk mengubah bilangan desimal menjadi bilangan heksadesimal, dapat dilakukan dengan cara membagi bilangan desimal tersebut dengan 16. Sebagai contoh, untuk mengubah bilangan 340810 menjadi bilangan heksadesimal, dilakukan dengan langkah-langkah sebagai berikut :

3409/16     =       213,         sisa   110            =          116, LSB

213/16  =     13,  sisa   510 =   516

13/16    =       0,  sisa 1310 =   D16, MSB

Sehingga, 340910 = D5116.

. Bilangan Hexsadesimal dan Biner

Setiap digit pada bilangan heksadesimal dapat disajikan dengan empat buah bit.

Untuk mengubah bilangan heksadesimal menjadi bilangan biner, setiap digit dari bilangan heksadesimal diubah secara terpisah ke dalam empat bit bilangan biner. Sebagai contoh, 2A5C16 dapat diubah ke bilangan biner sebagai berikut.

216  =   0010, MSB

A16  =   1010

516  =   0101

C16 =   1100, LSB

Sehingga, bilangan heksadesimal 2A5C akan diubah menjaid bilngan biner 0010 1010 0101 1100.

Sebaliknya, bilangan biner dapat diubah menjadi bilangan heksadesimal dengan cara mengelompokkan setiap empat digit dari bilangan biner tersebut dimulai dari sigit paling kanan. Sebagai contoh, 01001111010111002 dapat dikelompokkan menjadi 0100 1111 0101 1110. Sehingga:

01002  =  416, MSB

11112  =  F16

01012  =  516

11102  =  E16, LSB

Dengan demikian, bilangan 01001111010111002 = 4F5E16.

D. Bilangan Biner Pecahan
Dalam sistem bilangan desimal, bilangan pecahan disajikan dengan menggunakan titik desimal. Digit-digit yang berada di sebelah kiri titik desimal mempunyai nilai eksponen yang semakin besar, dan digit-digit yang berada di sebelah kanan titik desimal mempunyai nilai eksponen yang semakin kecil. Sehingga

0.110    =  10-1            =   1/10

0.1010 =  10-2‑               =   1/100

0.2       =  2 x 0.1       =   2 x 10-1, dan seterusnya.

Cara yang sama juga bisa digunakan untuk menyajikan bilangan biner pecahan. Sehingga,

0.12     =  2-1               =   ½, dan

0.012   =  2-2‑                  =   ½2  = ¼

Sebagai contoh,

0.1112     =   ½ + ¼ + 1/8

                 =   0.5 + 0.25 + 0.125

                 =   0.87510

101.1012 =   4 + 0 + 1+ ½ + 0 + 1/8

                 =   5 + 0.625

                 =   5.62510

Pengubahan bilangan pecahan dari desimal ke biner dapat dilakukan dengan cara mengalihkan bagian pecahan dari bilangan desimal tersebut dengan 2, bagian bulat dari hasil perkalian merupakan pecahan dalam bit biner. Proses perkalian diteruskan pada sisa sebelumnya sampai hasil perkalian sama dengan 1 atau sampai ketelitian yang diinginkan. Bit biner pertama yang diperoleh merupakan MSB dari bilangan biner pecahan. Sebagai contoh, untuk mengubah 0.62510 menjadi bilangan biner dapat dilaksanakan dengan

0.625 x 2   =   1.25,   bagian bulat    =         1 (MSB), sisa = 0.25

0.25 x 2     =   0.5,     bagian bulat    =         0, sisa = 0.5

0.5 x 2       =   1.0,     bagian bulat    =         1 (LSB), tanpa sisa

Sehingga,

0.62510      =   0.1012

E. Sistem Bilangan BCD
Sampai saat ini kita hanya melihat pengubahan dari bilangan desimal ke bilangan biner murni. Pada beberapa aplikasi, misalnya sistem berdasar mikroprosesor, seringkali lebih sesuai apabila setiap digit bilangan desimal diubah menjadi 4 digit bilangan biner. Dengan cara ini, suatu bilangan desimal 2 digit akan diubah menjadi dua kelompok empat

digit bilangan biner, sehingga keseluruhannya menjadi 8 bit, tidak bergantung pada nilai bilangan desimalnya sendiri. Hasilnya sering disebut sebagai binary-coded decimal (BCD). Penyandian yang sering digunakan dikenal sebagai sandi 8421BCD. Selain penyandian 8421BCD, juga dikenal sejumlah penyandian yang lain.

Contoh

Ubah 25.12510 menjadi bilangan biner

Penyelesaian

Pertama kali, lihat bagian bulat dari bilangan di atas, yaitu 25

25 / 2     =   12,  sisa 1, LSB

12 / 2     =   6,   sisa 0

6/ 2        =   3,   sisa 0

3/ 2        =   1,   sisa 1

1 / 2       =   0,   sisa 1

Sehingga, 2510    =     110012

Sekarang lihat bagian pecahannya, yaitu 0.125

0.125 x 2   =   0.25,   bagian bulat    =         0 (MSB), sisa 0.25

0.25 x 2     =   0.5,     bagian bulat    =         0, sisa 0.5

0.5 x 2       =   1.0,     bagian bulat    =         1, tanpa sisa

Sehingga 0.12510    =          0.0012

Secara keseluruhan 25.12510                =  11001.0012

Kode promo tokopedia

Kode promo tokopedia
Voucher diskon
Casback 50%
Casback hingga 30rb
Hai. Cobain Aplikasi Tokopedia, yuk! Bisa belanja dengan harga terbaik, isi pulsa atau bayar tagihan ini itu juga mudah. Download sekarang & nikmati cashback s.d 30rb untuk transaksi pertamamu.

                      Kode: TPARI9910. 

Cek: https://tokopedia.link/TPARI9910
Berlaku dari 12-12-2017

13-01-2018 bisa
14-02-2018bisa
15-03-2018 bisa
17-04-2018bisa
18-05-2018 bisa
19-06-2018bisa
20-07-2018 bisa
21-08-2018bisa
22-09-2018 bisa
26-09-2018 belum ada yang coba
27-09-2018 belum ada yang coba
28-09-2018
29-09-2018
30-09-2018
01-10-2018

Sampai tahun 2020

#voucher sekali pakai

harmonika #rangkuman

sejarah harmonika

Berbicara tentang sejarah, banyak sekali sumber-sumber yang bisa didapatkan mengenai kronologis sejarah itu sendiri. Begitu pula sejarah untuk harmonika, alat musik mungil nan unyu ini mempunyai sejarah tersendiri yang sudah banyak tersebar di berbagai macam sumber yang isinya juga kebanyakan mempunyai kemiripan. 

Harmonika adalah sebuah alat musik yang paling mudah dimainkan. Hanya tinggal meniup dan menghisapnya harmonika akan mengeluarkan suara yang cukup bagus. Harmonika berasal dari alat musik tradisional China yang bernama 'Sheng' yang telah digunakan kira-kira 5000 tahun yang lalu sejak kekaisaran Nyu-kwa.

Harmonika modern ditemukan pada tahun 1821 oleh Christian Friedrich Buschmann. Sebuah instrumen musik tiup sederhana yang terdiri dari plat-plat getar dari logam yang disusun secara horozontal dengan desain yang kurang baik dan hanya menyediakan nada tiup kromatis.

Desain awal dari Buschmann akhirnya banyak ditiru dan dimodifikasi menjadi lebih baik. Salah satu contohnya adalah harmonika buatan Richter yang merupakan desain awal dari sebuah harmonika modern. Pada tahun 1826 ia mengembangkan variasi harmonika dengan 10 lubang tetap dan 20 pelat getar dengan pemisahan fungsi pelat yang ditiup dan yang dihisap. Pada akhirnya, nada yang dibuat oleh Richter disebut sebagai nada diatonis dan merupakan nada standard harmonika.

Tahun 1847 Keluarga Seydel "Johann Christian Seydel dan Christian August Seydel" yang sebelumnya adalah keluarga penambang di Sachsenberg-Georgenthal /Saxony mulai mengembangkan usaha pembuatan instrumen harmonika di karenakan kegiatan usaha penambangannya yang dihentikan.

Pabrik pembuatan harmonika di tempatkan di Klingenthal di bawah kaki gunung 'Aschberg', selanjutnya seydel semakin mngukuhkan diri sebagai pabrikan harmonika di seluruh wilayah Saxony.

Tahun 1857 saat pengrajin jam Jerman bernama Matthias Hohner memutuskan untuk menjadi produsen harmonika. Dengan bantuan dari keluarganya, ia dapat memproduksi 650 harmonika tahun itu. Hohner memperkenalkan harmonika ke Amerika Utara pada 1862 sebuah langkah yang membawa pabrikan Hohner menjadi produsen nomor satu utnuk harmonika. Pada 1887 Hohner telah memproduksi lebih dari 1 juta harmonika per tahunnya. Sekarang, Hohner telah memproduksi lebih dari 90 model harmonika yang berbeda jenis, nada, dan model. Yang memungkinkan untuk memainkan berbagai macam gaya musik mulai dari pop, blues, rock, country, ska dan bermacam-macam lainnya.(Dari wikipedia dan duniaharmonika.blogspot)

Harmonica Signature Series

Disamping harmonika yang biasa kita lihat pada umumnya, terdapat beberapa harmonika yang diproduksi untuk mengapresiasi para musisi dunia yang telah mempopulerkan alat musik mungil ini. Dalam label Harmonica Signature Series, pabrikan harmonika kenamaan Hohner mengeluarkan setidaknya 4 harmonika kece yang dihiasi dengan tanda tangan harpist legend tersebut.
Berikut ke-4 harmonika signature series tersebut:
1. Harmonica Bob Dylan Signature Series

Bob Dylan

Bob Dylan adalah musisi kenamaan dari Amerika Serikat, lair di Minnesota 24 Mei 1941. Sudah mempunyai bakat musik sejak masih anak-anak dan mahir memainkan gitar dan harmonika. Majalah musik Rolling Stone menempatkan Bob dylan dalam urutan kedua pada daftar "Greatest Artists of All Time". Dylan hanya kalah satu tingkat tepat dibawah The Beatles, padahal sejatinya band yang dipimpin John dan Paul ini termasuk band yang terpengaruh gaya bermusik Dylan dan sering mendengarkan lagu - lagu milik Dylan.
Dan Hohner secara khusus memproduksi Harmonica Signature Series Bob Dylan.. berikut beberapa penampakannya:

Bob Dylan Harp Box

Bob Dylan Sign Series

Harmonika seri Bob Dylan bisa sahabat harmoncalovers dapatkan di toko musik atau di online shop dengan banderol harga +/- Rp. 950.000,-

2. Harmonica J.J Milteau Signature Series 

JJ. Milteau

Mungkin bagi kita nama Jean Jacques Milteau masih terdengar asing di telinga kita. Namun di negara asalnya Perancis dan di belahan eropa lainnya nama JJ Milteau cukup dikenal sebagai seorang harpist handal. Tertarik pertama kali dengan harmonika ketika mendengar musik rock (Bob Dylan dan Rolling Stones) pada tahun 1960. Dan secara khusus Hohner pun memproduksi Harmonica JJ Milteau Signature Series

Hohner J.J Milteau Deep Blues

JJ Milteau Sign Series Harmonica

Harp ini bisa sahabat harmonicalovers dapatkan di toko musik terdekat (bila ada) dg kisaran harga +/- Rp. 350.000,-

3. Harmonica Steve Tyler Signature Series

Steve Tyler

Pasti sudah tidak asing lagi dengan om Steve Tyler ini dong? yups, dia adalah vocalis Aerosmith yg jg jago main harmonika. Dan Hohner pun memproduksi juga Sign Series Steve Tyler.. penampakannya nih

  

Harmonika ini kemungkinan masih belum beredar di Indonesia. Bisa didapatkan di situs belanja online luar negeri. Untuk kisaran harganya adalah $52,95 *amazone.com*

4. Harmonica John Lennon Signature Series

John Lennon

Nah.. kalau musisi yang satu ini pasti sudah pada tahu dong.. personil band legendaris @thebeatles.. yups, opa John Lennon.. Selain terkenal mahir menciptakan lagu, dunia juga mengagumi permainan harmonika si jenius yang satu ini. Permainan ciamiknya dalam meniup harmonika bisa didengarkan dibeberapa lagu The Beatles seperti Love Me Do, From Me To You, dll

Hohner pun mengapresiasi karya2nya lewat Sign Series-nya.. dengan nama IMAGINE membuat harp ini begitu elegan.

IMAGINE John Lennon

John Lennon Signature Series

Harmonika kece ini bisa kalian dapatkan dengan harga +/- Rp. 800.000,- dan sudah beredar di Indonesia

Bagaimana sahabat harmonicalovers? Tertarik untuk memiliki salah satu harmonika di atas? Nabung ya.. hehe.. Salam harmonicalovers semuanya, jangan lupa tinggalin jejak kalian di kolom komentar ya :)

sumber:

akun twitter @harmonicalovers

wikipedia.com

tokobagus.com

kaskus.com

Jenis-jenis Harmonika

Terdapat beberapa jenis harmonika yang bisa kita lihat dengan cara membedakan bentuk fisik dari harmonika itu sendiri. Di Indonesia, mayoritas hanya ada 3 jenis harmonika yang beredar di pasaran dan cukup mudah untuk ditemui di berbagai toko musik. Walaupun sebenarnya ada lebih dari 3 jenis harmonika yang dimaksud, namun pada tulisan ini akan lebih menitikberatkan pada ketiga jenis harmonika tersebut.

1. Harmonika Tremolo (Tremolo Harp)

Mempunyai ciri lubang yang bersusun dempet dan body yang panjang seperti gambar di atas. Hal ini terjadi karena umumnya harmonika jenis ini punya 12 semitone yang bisa kita mainkan. Fungsi dari harmonika jenis ini sesuai namanya untuk memberikan efek gema atau berulang pada nada yang kita mainkan. Biasanya untuk bermain musik Classic dan Harmonica Group bareng sama Chromatic dan Chord Harp di bawah , jarang digunakan untuk permainan solo.

Peredaran harmonika tremolo ini lebih banyak mencakup kalangan menengah ke bawah karena cara bermain yg mudah & harga yg terjangkau. Harmonika tremolo ini rata-rata dijual di pasaran dg harga mulai dari Rp. 25 ribu - Rp. 80-an ribu.. tergantung merknya, karena ada pula yang harganya dibanderol melebihi harga tersebut.

2. Harmonika Diatonik (Diatonic Harp)

Mempunyai 10 lubang tanpa sekat atas bawah seperti yg ada pada harp tremolo, harmonika ini punya modal Richter-tuned yang artinya memungkinkan kita untuk memainkan 1 kunci harmonika di beberapa chord yang berbeda. Biasanya dipakai untuk mengiringi jenis musik Blues, Country, dan Folk, tapi tidak menutup kemungkinan juga bisa diterapkan ke Jazz ataupun Classic.

Harmonika diatonik ini rata-rata dijual di pasaran dg harga mulai dari Rp. 70an ribu - > Rp. 500an ribu.. tergantung merknya juga.

3. Harmonika Kromatik (Chromatic Harp)

Dilihat dari bentuknya sudah jelas kelihatan berbeda dari harmonika diatonik maupun tremolo. Ada tombol (pencetan) di sampingnya. Itu gunanya untuk menggeser slide penutup lubang yang ada untuk menghasilkan nada-nada kres. Contohnya di lubang nomer 3 itu bunyinya C berarti kalau kita tekan tombol itu maka bunyinya bisa jadi C# atau Db. Biasanya dipakai buat mengiringi jenis musik Pop, jazz, dan Classic.

Harmonika jenis ini mempunyai harga yg lebih mahal dibandingkan dengan harmonika jenis lain. kromatik ini rata-rata dijual di pasaran dg harga mulai dari Rp. 1 jt - > Rp. 2,5 jt.. tergantung merknya juga. 

dikutip dari berbagai sumber

Buku Panduan Harmonicalovers

Sudah pernah mencari buku panduan cara bermain harmonika? Sesekali, sering atau memang tidak pernah sama sekali? Bagi sahabat harmonicalovers yang pengen banget belajar bermain harmonika, tidak jarang mencari panduan2 bermain harmonika melalui internet baik itu dari video tutorial atau panduan tertulis. Namun untuk buku panduan belajar harmonika berbahasa Indonesia sangat jarang ditemui atau bahkan bisa dikatakan tidak ada sama sekali. Paling banyak adalah buku panduan belajar bermain gitar ataupun piano.

Nah, mulai bulan Januari 2013 ini sahabat harmonicalovers bisa sedikit tersenyum dengan terbitnya buku panduan belajar harmonika yang berbahasa Indonesia. Buku dengan judul Cara Mudah Mahir Main Harmonika ini sudah beredar di pasaran dan yang pasti bertujuan untuk mempermudah belajar harmonika

Penampakan buku Mahir Main Harmonika

berikut review dari buku di atas:
Buku #MahirMainHarmonika ini memang diperuntukkan untuk pemula karena buku ini berisi pengenalan harmonika beserta kunci-kunci dasarnya. 
Buku ini terbagi menjadi 4 bab yang di tiap-tiap bab-nya sahabat harmonicalovers akan diajak berkenalan dengan harmonika lebih jauh.
Pada bab pertama pembaca akan diajak mengenali apa itu alat musik harmonika yg masih terdengar asing di telinga masyarakat luas.
Pada bab kedua, pembaca akan diajak mengenali jenis-jenis harmonika dan cara mudah bermain harmonika.
Di bab ketiga, pembaca akan dikenalkan pada berbagai macam kunci harmonika mulai dari diatonik, tremolo, dan kromatik 
Pada bab terakhir, pembaca akan diajak untuk memainkan harmonika pada musik rock, pop, dan klasik disertai tab lagu untuk harmonika diatonik, kromatik, dan tremolo.
Buku ini secara umum tidak direkomendasikan untuk pemain profesional dikarenakan buku ini cukup tipis dan hanya membahas pokok2 penting terkait kunci dan cara memainkan harmonika.

Sahabat harmonicalovers bisa mendapatkan buku #MahirMainHarmonika ini dengan harga yang cukup terjangkau yakni Rp. 25.000,- dan didapatkan di toko buku Gramedia terdekat.

Tips Membeli Harmonika

Menjadi seorang harpist legend? Harpist terkenal? Atau pemain harmonica handal? Semua itu bisa kita lakukan dengan cara rutin latihan dan terus latihan. Namun ada satu hal terpenting yang harus dilakukan oleh seseorang untuk menjadi hal seperti di atas, yakni mempunyai sebuah harmonica.

Ya, tanpa adanya harmonica, mana mungkin seseorang bisa latihan tanpa suatu alat bantu? Sebenarnya bisa dengan meminjam harmonica pada seseorang, tapi apakah kita tidak malu meminjamnya terus menerus karena harmonica pada hakekatnya adalah alat music pribadi yang tidak boleh berpindah mulut jika tidak ingin terkena virus bau mulut orang lain. Hehehe.. :p

Jadi, hanya dengan satu cara yakni dengan membeli sebuah harmonica agar impian dan harapan kita menjadi seorang harpist handal bisa dengan cepat segera terwujud. Berikut ini beberapa tips yang mungkin bisa dijadikan rujukan bagi sahabat harmonicalovers sebelum memutuskan membeli sebuah harmonica, terutama bagi yang pertama kali ingin membeli harmonika.

1. Cari tahu tentang berbagai jenis harmonica. Karena harmonica mempunyai beberapa jenis yang pastinya mempunyai ciri dan fungsi yang berbeda. Ada harmonica tremolo, diatonic, dan kromatik yang banyak beredar di pasaran. Pilih yang cocok dengan karakter dan kemampuan kalian. (lihat postingan sebelumnya)

2. Cari tahu juga tentang kunci harmonica. Fyi, harmonica bukanlah alat music yang semuanya mempunyai letak nada yang sama seperti halnya piano, gitar, seruling, dsb. Ada banyak sekali macam kunci pada harmonica terutama harmonica diatonic. Untuk pemula biasanya disarankan memilih harmonica kunci C. (lihat postingan sebelumnya)

3. Sesuaikan dengan budget atau uang yang ada di kantong. Ini salah satu bagian yang penting dalam membeli sebuah harmonica, jangan sampai harmonica yang kalian beli harganya melebihi budget yang kalian miliki. Cari tahu info tentang harga harmonica yang ingin kalian beli. Jangan muluk-muluk membeli harmonica dengan harga mahal kalau pada akhirnya tidak terpakai. Beli harmonica yang murah tapi tidak murahan. (lihat postingan sebelumnya)

 Jadi, udah siap membeli harmonika?

Bagian-bagian Harmonika

Sahabat harmonicalovers ada yang tahu dengan bagian-bagian atau komponen yg digunakan dalam membentuk sebuah harmonika? Mungkin ada yang mengira bahwa hanya sekadar penutup harmonika dan bagian dalamnya saja. Namun jika diperhatikan lebih mendalam, ada beberapa komponen atau bagian yg bisa kita lihat sebagai unsur pembentuk harmonika.

Kita bisa melihat gambar berikut

Dari gambar di atas, kita bisa melihat ada 5 bagian yang terbagi dalam 3 komponen dasar pembentuk harmonika. 2 bagian penutup (top cover dan bottom cover), 2 bagian reeds (blow reeds dan draw reeds), dan 1 bagian di tengah yang disebut dengan comb.

Berikut penjelasan masing-masing komponen pada harmonika

Ø  Reed (pelat/buluh getar)

Bagian ini adalah bagian yang sangat vital dalam sebuah harmonika, karena bagian inilah yang akan menghasilkan bunyi bila dilewati aliran udara dan bergetar. Reed ini tersusun secara rapi pada sebuah lempengan, dan semakin panjang reed, maka semakin rendah nada yang dihasilkannya. Sebaliknya, semakin pendek reed, maka nada yang dihasilkan akan semakin tinggi.

Ø  Reed Plate

Bagian yang berbentuk lempengan logam ini adalah tempat menempelnya pelat-pelat getar. Dalam sebuah harmonika, ada dua buah lempengan logam ini. Yang pertama adalah lempengan logam tempat menempelnya pelat-pelat getar nada-nada tiup (blow reed), sedangkan yang ke dua adalah tempat menempelnya pelat-pelat getar nada-nada sedot (draw reed). Dapat Anda perhatikan bahwa pada setiap pelat getar, selalu ada "coakan" atau lubang dengan ukuran yang hampir sama dengan pelat getar, dan berfungsi sebagai ruang tempat pelat getar melakukan gerakan naik turun ketika ada aliran udara yang melewatinya. Coakan ini sering disebut dengan "Reed Slot". Celah antara coakan dan pelat getar tersebut akan sangat berpengaruh terhadap kekedapan udara (airtightness) sebuah harmonika.

Ø  Comb

Comb dalam bahasa Inggris berarti sisir. Ya... komponen ini disebut demikian karena bentuknya memang mirip dengan sisir. Comb menjadi tempat dipasangnya reed plate dan cover plate. Pada komponen inilah, lubang-lubang sedot/tiup berada. Dapat Anda lihat, pada bagian dalam comb, terdapat ruang-ruang yang panjangnya mengikuti panjang setiap reed. Ruang-ruang inilah yang menjadi  tempat terbentuknya kolom-kolom udara, yang akan menggetarkan reed dan menghasilkan bunyi.

Ø  Cover Plate

Komponen ini adalah komponen yang paling mudah dilihat pada sebuah harmonika. Selain menjadi penutup reed plate dan comb, bagian ini berfungsi sebagai tempat terjadinya resonansi nada yang dihasilkan oleh reed. Dengan adanya resonansi ini, maka nada yang dihasilkan akan terdengar lebih keras. Tanpa cover plate, sebenarnya bunyi yang dihasilkan oleh reed akan tetap terdengar, namun tak sekeras bila cover plate dipasang. Pada bagian ini jugalah, logo/merk dan angka lubang sebuah harmonika dicetak.

nah, sudah tahu kan bagian-bagian dari harmonika?
jadi, jika kalian ingin membuka harmonika dan membersihkan bagian dalam harmonika, kalian tidak akan bingung lagi dengan bagian-bagian dalam harmonika. 
 
dikutip dari http://www.harp-monica.blogspot.com/

Harmonika Unik

Secara umum, ketika mendengar kata "harmonika", yang terlintas di benak kita adalah sebuah alat musik yang berukuran kecil dengan bentuk balok yang terdapat lubang-lubang untuk menghasilkan suara. Namun dari kebanyakan harmonika dengan bentuk yang lazim seperti deskripsi di atas, ada beberapa bentuk harmonika unik yang berbeda dari biasanya dan bahkan mempunyai fungsi lain selain sebagai alat musik tiup.

Berikut beberapa harmonika unik dengan bentuk dan fungsi yang berbeda dari harmonika pada umumnya, tapi yang pasti fungsi sebagai alat musik tiup sedot tidak dapat dihilangkan..

1. Gantungan kunci Harmonika
Gantungan kunci dengan bentuk harmonika ini bisa dijadikan aksesoris unik maupun koleksi bagi pencinta harmonika karena selain ukurannya lebih kecil dari harmonika pada umumnya, juga bisa dijadikan sebagai gantungan kunci pada motor, mobil, pintu, dsb seperti nama benda ini.

2. Pink Harmonika
Sebenarnya harmonika ini tidak berbeda dengan harmonika-harmonika lainnya yang hanya memiliki fungsi sebagai alat musik tiup-sedot. Namun karena warnanya merah jambu atau yang biasa dikenal dengan warna pink membuat harmonika ini lain daripada yang lain. Tentunya para harpist angel atau pencinta harmonika perempuan lebih tertarik untuk memiliki harmonika ini.

3. Harmonika Kaca
Dilihat dari bentuknya, harmonika ini paling berbeda dengan harmonika lainnya. Cara memainkannya pun berbeda pula. Jika pada harmonika normal dengan meniupnya bisa mengeluarkan suara, maka pada harmonika kaca ini cara memainkannya seperti bermain sebuah piano.

4. Flashdisk Harmonica
Sebenarnya masih bingung juga tentang konsep benda ini. Flashdisk berbentuk harmonika atau harmonika dengan fungsi tambahan sebagai flashdisk? Hahaha.. Yang jelas, benda ini cukup menarik perhatian banyak orang terutama bagi pencinta harmonika. Tapi kayaknya memang ini adalah flashdisk yang berbentuk harmonika. Bisa berfungsi sebagai flashdisk yg menyimpan berbagai macam file, bisa pula dimainkan layaknya sebuah harmonika. Waaah.. Keren ya..

5. Six Side Harmonica
Ada 6 buah harmonika yang digabung menjadi satu. Kalau nggak salah sih tiap harmonika memiliki kunci yang berbeda. Jadi nggak perlu repot-repot bawa 6 buah harmonika kalo punya harmonika ini. Tapi, mahal banget lho harganya..

6. Chord Harmonica
Harmonika ini bisa dikatakan sebagai nenek moyangnya harmonika. Dari sekian banyak sumber dan tulisan tentang jenis-jenis harmonika, Chord harmonica adalah satu dari 4 jenis harmonika yang ada di pasaran. Harmonika ini mempunyai bentuk yang sangat besar. Lihat saja penampakannya.

7. Harmonika Terompet
Dilihat dari bentuknya bisa disimpulkan bahwa benda ini adalah gabungan dari dua alat musik yaitu harmonika dan terompet. Mungkin sang penciptanya berpikiran kalau dua alat musik ini digabungkan akan menghasilkan suara yang lebih nyaring seperti suara yang dihasilkan oleh terompet

8. Kalung Harmonika
Bagi pencinta harmonika yang tidak ingin jauh-jauh dari penda kesayangannya bisa mencari barang ini, karena dengan adanya penambahan aksesoris sebuah kalung membuat harmonika tidak akan pernah jauh dari pemiliknya dan tentu saja bisa dimainkan kapan dan di mana saja.

9. Harmonika Mini
Dengan ukuran yang sangat kecil membuat peniupnya harus me"monyong"kan bibir lebih kedalam untuk bisa memainkannya.

10. Tremolo-Chromatic Harmonica
Dengan bentuk yang unik membuat harmonika ini berbeda dari harmonika pada umumnya.

Belajar Bending Harmonika

Apa itu Bending?

Note bending adalah teknik yang digunakan untuk mengubah pitch note dan sebagainya mencapai note yang tidak ada padaharmonika diatonik, Misalnya, jika sahabat #harmonicalovers mengambil lubang keempat pada harmonika kunci C, nada tiup adalah C dannada sedot adalah D. Hal ini dimungkinkan untuk memainkan nada C# dengan membending lubang ke 4 dengan satu setengah nada. Hal ini bisa dilakukan dengan menggunakan kombinasi lidah, tenggorokan dan paru-paru untuk memvariasikan tekanan udara pada reed harmonika. 

Bending menjadi salah satu teknik yang lebih sulit untuk dikuasai (butuh waktu yang cukup lama) tapi itu sepadan dengan usahanya. Perhatikan bahwa membending adalah menghasilkan suara blues yang ada pada harmonika, dan dapat digunakan dalam kombinasi dengan efek lain seperti wah-wah untuk menambah gaya dan keragaman bermain sahabat #harmonicalovers. Meniup lubang ke 4 adalah nadapertama yang dipelajari untuk membending tapi ini tidak berlaku untuk semua orang. Jika Anda memiliki banyak kesulitan, berlatihlahmembending pada lubang lain (baik, 1 sedot, 2 sedot atau 3 sedot).

Harmonika yg admin ambil sebagai contoh adalah harmonika diatonik key C. Terutama pada hamonika diatonik, ada beberapa nada yg hilang (tidak tersedia) yang cara menemukannya harus melalui bending. Coba perhatikan tab not key C berikut yang memang ada nada yg hilang (F pada lubang 2) 

tab-note diatonic harp key C

 berikut teknik-teknik bending yang harus dilakukan oleh pemain harmonika agar bisa mendapatkan nada-nada yang hilang seperti  yang ada pada warna hijau dan merah muda pada gambar di atas.

 

Bending Lubang 4, dari D turun ke C#

Kita akan langsung membahas bagaimana secara fisik melakukan teknik bending. Dimulai pada lubang ke 4 dengan melakukan bending sedot/hirup pada harmonika diatonic kunci C. Ini adalah membending nada D ke C #.

Dengarkan terlebih dahulu tutorial berikut ini (bs di download)

bending sedot lubang 4

 

Sekarang sahabat #harmonicalovers sudah tahu setelah mendengar dan kita akan menjelaskan bagaimana hal itu dilakukan (folk yang berbeda memiliki cara yang berbeda untuk menggambarkan bagaimana membending nada). Perhatikan gerakan lidah pada gambar di bawah ini. Sementara kita menghirup pada lubang keempat, kita mencelupkan tengah lidah kita turun meninggalkan ruang yang lebih besardi dalam mulut kita. Tindakan mencelupkan lidah kita turun membawa nada dari D ke C #.

four hole bend

Hal ini mungkin sulit dilakukan karena akan melatih lidah kita untuk melakukan sesuatu yang tidak biasa karena belum pernah melakukan sebelumnya. Tetapi ketika kita dapat menguasainya, maka akan semudah mengendarai sepeda. Ada beberapa trik yang mungkinbisa membantu.

             Dapatkah sahabat #harmonicalovers bersiul mundur? (bersiul dengan cara menghirup). Kalian akan melihat bahwa kalianmemindahkan lidah kalian kembali ke dalam mulut kalian, sehingga meningkatkan volume rongga atau ruang di dalam mulut kalian. Ini adalah efek yang sama, tetapi kalian akan melakukan hal ini sementara meninggalkan lidah kalian pada harmonika. Kita harus mampumeninggalkan lidah kita pada harmonika, sehingga kita dapat membending nada sedangkan lidah kita menghalangi (gaya bermain yangdijelaskan pada pelajaran sebelumnya).

Ketika kita pertama kali mencoba untuk membending nada, itu tidak datang kepada kita secara langsung. Salah satu hal yang dapat kita lakukan adalah dengan menempatkan beberapa scotch tape (selotip atau tape lengket) di depan harmonika, sehingga memblokir semualubang kecuali satu, kita berlatih terus-menerus. Ini berarti bahwa kita bisa melakukan teknik bending menggunakan metode bersiul mundur (mundur peluit), dan tidak khawatir tentang pemblokiran lidah. Jika kita mengalami kesulitan membending nada sedangkan lidah memblokir, latihan ini akan memberikan suara dan nuansa bermain bending nada. Meskipun di sisi lain, kita benar-benar tidak ingin menutupi harmonikadengan scotch tape jika kita bisa menghindarinya.

Bending Lubang 3, dari B turun ke Bb, A dan Ab

Menghirup lubang ke-3 pada harmonika kunci C dapat di bending ke dalam tiga tahap nada masing-masing setengah nada. Dengarkan rekaman berikut ini untuk mendengar bagaimana bunyinya.

 bending sedot lubang 3

 

Gambar di bawah menunjukkan posisi berbagai lidah nada di lubang ini.

three hole bend

Pertama nada B adalah nada lurus dan dapat dimainkan hanya dengan menghirup pada lubang ketiga harmonika kita. Kita kemudian dapat menurunkan pitch nada ini ke nada Bb, A, dan Ab, dengan mencelupkan pusat lidah kita ke dalam tiga tahap. Kita mungkin merasa sulit untuk mengetahui apakah kita mendarat tepat pada setiap nada setengah, jadi latihan lain yang baik adalah untuk menyelesaikan pada 3 nada tiup. Finishing pada 3 nada tiup akan berarti bahwa kita bermain 5 nada dari skala kromatik pada satu lubang harmonika kita, B, Bb, A, Ab, dan G. Ini akan membuat lebih mudah bagi kita untuk mendengar jika kita jarak mereka terpisah dengan benar (satu setengah nadamasing-masing).

bending sedot lubang 3 ke G 

Bending Lubang 2, dari G turun ke F#, dan F

Menghirup lubang kedua pada harmonika kunci C dapat dibending ke dalam dua tahap nada masing-masing setengah nada. Dengarkan rekaman berikut ini untuk mendengar bagaimana bunyinya.

bending sedot lubang 2 

Gambar di bawah menunjukkan posisi berbagai lidah nada di lubang ini.

two hole bend

 Pertama nada G adalah nada lurus dan dapat dimainkan hanya dengan menghirup pada lubang kedua harmonika kita. Kitakemudian dapat menurunkan pitch nada ini ke F # dan F, dengan mencelupkan pusat lidah Anda ke dalam dua tahap.

             Ketika kita mulai untuk mendapatkan nuansa bending yang berbeda kita akan melihat bahwa setiap lubang memiliki bentuk yang berbeda hingga yang terakhir. Reeds yang lebih besar di bagian bawah lubang bernada memungkinkan aliran yang lebih besar dari udara melalui harmonika ke paru-paru kita. Ini berarti bahwa kita akan menghirup lebih besar volume udara untuk mencapai perbedaan tekanan yang dibutuhkan untuk mencapai bending. Ini akan sangat terlihat pada lubang pertama.

Bending Lubang 1, 5 dan 6

Nada hirup pada lubang pertama harmonica kunci C kita dapat dibending turun setengah nada dari D ke C #. Ini adalah nada yang sama seperti yang kita melakukan bending pada lubang keempat, tetapi lubang pertama ini satu oktaf lebih rendah daripada lubang keempat. Kita akan melihat bahwa kita menghirup lebih banyak udara saat melakukan bending di lubang pertama ini. Kita tidak perlu khawatir tentangpemblokiran lidah pada lubang pertama, sehingga kita dapat menarik lidah kita kembali ke dalam mulut kita jika ini membuat lebih mudah.

Bending di lubang pertama harus terdengar seperti ini.

bending sedot lubang 1 

 

Kita akan mampu melakukan bending pada lubang ke 5 turun dari E, tapi ini kurang dari setengah nada (meskipun terdengar sepertiF). Bending ini dapat digunakan untuk efek, tetapi tidak boleh digunakan untuk bermain catatan F.

             Menghirup nada pada lubang keenam pada harmonika kunci C kita dapat dibengkokkan oleh nada setengah dari A ke Ab, dan harusterdengar seperti ini.

bending sedot lubang 6 

 

Gambar di bawah ini untuk menggambarkan semua kemungkinan bending pada harmonika. Kita baru saja membahas bending sedotdari lubang 1 sampai 6. Ketika belajar cara bermain harmonika, pemula pada umumnya menemukan bending tiup pada lubang 8 sampai 10yang lebih sulit. Jadi untuk latihan berikutnya kita akan berbicara tentang beberapa teknik yang dapat digunakan dalam kombinasi denganbending.

Wah-wah

Efek wah-wah dapat dicapai dengan membuka dan menutup tangan kita di bagian belakang harmonika. Ketika dilakukan kombinasi dengan membending nada efeknya dapat ditingkatkan. Rekaman pertama adalah hanya menghirup lubang ke 4 tanpa bending (nada D).

 wah_wah

Sekarang! Kali ini, kita mulai pada lubang ke 4 hirup bending nada C #, dan melepaskannya lurus 4 hirup (dari nada C # ke D). Lakukan ini berulang-ulang sehingga terdengar seperti wah-wah. Kemudian tambahkan efek wah-wah.

 bend_plus_wah_wah

 

Ps: kita mungkin menyadari bahwa kita dapat mendengar anjing mengerang di latar belakang dekat akhir rekaman itu, abaikan saja.

 

Suara Kereta Api

Sebuah efek peluit kereta dapat dicapai jika Anda membending dua lubang secara bersama-sama. Tarik napas pada lubang 4 dan 5dan kemudian bending kedua nada tersebut secara bersama-sama.

 suara kereta api

 

Bending Tiup

Membending nada tiup "terasa" sama persis seperti membending nada hirup, namun kita akan menemukan sedikit kesulitan untuk menguasainya. Tidak ada gunanya berlatih teknik ini jika kita belum menguasai latihan sebelumnya. Jadi, berlatihlah teknik bending hirup sampai kita merasa sangat nyaman dengan itu.

Bending Tiup Lubang 8, dari E turun ke Eb.

Lubang ke 8 pada harmonika C dapat dibending dengan nada setengah dari nada E ke Eb.

 bending tiup lubang 8

 

Gambar di bawah ini menunjukkan apa yang kita rasakan dan kita lakukan. Kita mengangkat lidah di bagian belakang dan meniupdengan " ever so slightly " kekuatan lebih. Jika kita mengalami kesulitan akan lebih mudah jika kita mulai pada harmonika kunci rendah, seperti G atau A. Kita kemudian dapat melakukannya dengan harmonika kunci yang berbeda.

eight hole bend

Bending Tiup Lubang 9 dan 10.

Lubang 9 adalah pengalaman serupa tapi sedikit lebih sulit. Ini akan membending dari nada G ke F # (setengah nada).

bending tiup lubang 9

Bending tiup pada lubang ke 10 harmonika C, akan membending dari nada C ke Bb (nada penuh). Hal ini sangat sulit untuk dilakukan pada harmonika C

bending tiup lubang 10

Overblows and Overdraws

Sebuah pelajaran disiapkan oleh Foghorn

overblows an

Bermain Harmonika

Bermain harmonika bagi kebanyakan orang sepertinya kelihatan mudah karena hanya dengan meniup dan menyedotnya saja harmonika bisa menghasilkan nada-nada yang indah. Namun jangan disepelekan pula karena pada kenyataannya bermain harmonika tidak semudah seperti yang dibayangkan, dibutuhkan latihan dan kegigihan dari pemainnya untuk memainkan alat musik mungil ini.

Tidak hanya dengan sekadar meniup atau menyedotnya, kita bisa memainkan sebuah irama atau lagu yang merdu jika didengarkan. Bahkan jika kita memainkannya tetapi tidak tahu cara bermainnya, bisa-bisa kita akan mendapatkan hadiah sandal gratis dari orang yang mendengarkan permainan harmonika kita (baca: dilempar sandal)

Pertama-tama sebelum kita serius ingin belajar bermain harmonika, kita harus mempunyai harmonika dulu (bisa sih pinjam, tapi apa gak malu pinjam terus? hehe..). Ambillah sebuah harmonika, mainkan dengan cara tiup dan sedot untuk mendapatkan soulnya. :)

Oh ya, harmonika yang jadi tutor di sini adalah harmonika jenis diatonik kunci C yang lazim digunakan untuk para pemula.

Kemudian kita harus tahu cara memegang harmonika-nya. Sebenernya sih terserah kita mau megang harmonika seperti apa, yang jelas kita ngerasa nyaman ketika kita memainkannya.

Seperti yang telah disebutkan di atas, bermain harmonika tidak asal tiup-sedot saja karena ada rumus tersendiri untuk memainkannya.

Kita andaikan nada2 dg angka do=1, re=2, mi=3, dst.. jika T=Tiup S=Sedot maka dalam 1 tangga nada punya rumus T-S-T-S-T-S-S 

Jadi dalam prakteknya untuk memainkan 1 tangga nada pada harmonika adalah dengan cara T-S-T-S-T-S-S dengan catatan T=Tiup, S=Sedot

Dimulai dari lubang mana? karena yang menjadi tutorial adalah harmonika diatonik kunci C maka rumus diatas dimulai dari lubang ke-4 (beda kunci, beda pula letak nada yang dimainkan)

Pada dasarnya harmonika diatonik terdiri dr 10 lubang dengan 3 bagian nada (low, middle, high) not dengan catatan --> low = nada bass, middle = nada normal, high = nada tinggi

Untuk lebih jelasnya mengenai tangga nada pada harmonika bisa dilihat pada diagram harmonika (tab not) berikut

Khusus pada harmonika diatonik ini, tidak semua nada dapat dimunculkan seperti 1 tangga nada utuh pada bagian middle tone (nada normal). Ada beberapa nada yang hilang yang cara mencarinya dibutuhkan teknik bending yang akan kita pelajari pada bagian berikutnya.

Bagaimana sahabat #harmonicalovers? cukup mudah kan sebenarnya bermain harmonika itu? Hanya dengan cara rutin bermain harmonika dan latihan secara kontinyu bisa membuat kita mahir untuk bermain harmonika.

Masih bingung ya?

kalau punya facebook, join aja di grup pencinta harmonika

atau kalau kamu twitter addict, follow twitternya di @harmonicalovers

dikutip dari berbagai sumber

Tab Not Harmonika Diatonik all key

Pada postingan kali ini, admin akan membagi tab not atau diagram nada pada harmonika diatonik untuk semua kunci. Karena pada harmonika diatonik, beda kunci beda pula letak nada yang dihasilkan pada tiap lubangnya.
Masih ingat kan bentuk harmonika diatonik?

Berikut tab not pada harmonika diatonik :
1. Harmonika Diatonik kunci C

2. Harmonika Diatonik kunci D

3. Harmonika Diatonik kunci Db

4. Harmonika Diatonik kunci E

5. Harmonika Diatonik kunci Eb

6. Harmonika Diatonik kunci F

7. Harmonika Diatonik kunci F#

8. Harmonika Diatonik kunci G

9. Harmonika Diatonik kunci A

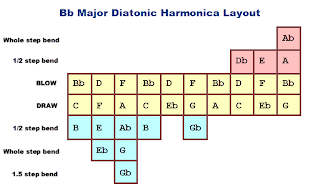
10. Harmonika Diatonik kunci Ab

11. Harmonika Diatonik kunci B

12. Harmonika Diatonik kunci Bb

Jadi, udah tahu letak-letak nada di masing-masing kunci pada harmonika diatonika kan? Semoga postingan ini bisa jadi bahan untuk belajar bagi sahabat #harmonicalovers semuanya, khususnya bagi pengguna harmonika diatonik..
Dan jangan lupa, follow twitter kita ya di @harmonicalovers :)

Membaca Tab Harmonika

6  5 -5  6  5  6  7 -7 -6  6  5  4 -6  6 -5  5  4 -4  5  5 -4
Waktu terasa semakin berlalu tinggalkan cerita tentang kita

6  5 -5  6  5  4  4  7 -7 -6  6  5  6 -6  6 -5  5  4 -4  5  5  5 -4
Akan tiada lagi kini tawamu tuk hapuskan semua sepi di hati


Bingung ya membaca tabulasi nada di atas?
Memang buat yang belum pernah melihat tab not harmonika masih bingung bagaimana cara membacanya. Bagaimana cara mengaplikasikannya pada harmonika?
Oke, di sini mari kita belajar cara membaca tab harmonika

Tab harmonika adalah serangkaian petunjuk yang dituliskan dengan angka untuk menunjukkan pada bagian lubang mana harmonika itu harus ditiup atau disedot. Dan biasanya sebelum not tabulasi itu diberikan, terdapat petunjuk untuk tipe harmonika dan kunci apakah tabulasi itu cocok dimainkan. Untuk harmonika diatonik biasanya angka tabulasinya maksimal sampai angka 10, untuk kromatik 12, dan tremolo 16 atau 24.

Dalam membaca tab harmonika, kita perlu memperhatikan angka yang ditunjukkan pada tab tersebut. Angka menunjukkan lubang mana yang harus ditiup atau disedot. Kemudian ketika kita melihat ada tanda (+) atau (-) pada tab tersebut, kita juga tidak boleh mengabaikannya. Tanda (+) *biasanya tidak disertakan dalam tab* menunjukkan bahwa lubang pada nomor tersebut cara memainkannya adalah dengan cara tiup. Sedangkan tanda (-) cara memainkannya adalah dengan cara disedot. Misalnya 5: lubang 5 ditiup dan -5 lubang 5 disedot.

Namun terkadang kita juga akan melihat akan ada tanda petik ( ' ) pada angka2 di tab tersebut. Hal ini diharuskan untuk melakukan bending pada lubang tersebut. *untuk teknik bending akan diuraikan di artikel selanjutnya*. Ada beberapa tanda petik yang bisa muncul pada sebuah tab harmonika karena  memang ada beberapa lubang yg bisa diturunkan hingga 1,5 nada. Misalnya -3''' jadi lubang ketiga harus dibending satu setengah nada.

Kita lihat penggalan tab nada diatas, 6  5 -5  6  5 menunjukkan bahwa lubang 6tiup, 5tiup, 5sedot, 6tiup, 5tiup dan seterusnya. Untuk lebih mengetahui macam2 lagu dengan tab harmonika, sahabat #harmonicalovers bisa mengunjungi situs tab harmonika. Ada ribuan lagu dg tab harmonika di sana, dan kalian bisa mempelajarinya jika ingin mengasah kemampuan bermain harmonika kalian.

Tapi jika Anda ingin menjadi pemain harmonika profesional, berhentilah membaca tab dan belajarlah bermain dengan mengandalkan pendengaran Anda sendiri (ear playing). *rona telam quite* harpist angel dari grup facebook pencinta harmonika.

sumber
disadur dari blog Rona Telam blog

Tips Merawat Harmonika

Harmonika adalah alat musik yang berbeda dengan alat musik lainnya karena memiliki ukuran yang lebih kecil sehingga membutuhkan perawatan yang khusus jika harmonika anda ingin selalu dalam kondisi yang baik.

Harmonika memiliki strip tipis dari logam yang jika bergetar maka akan menghasilkan suara. Ukuran bagian ini sangat tipis, sehingga jika ada kotoran yang menyangkut akan membuat suara yang duhasilkan harmonika menjadi tidak bagus.

Berikut ini adalah 8 hal yang bisa anda lakukan untuk menjaga harmonika anda tetap bersih :

1. Jangan makan sambil memainkan harmonika Anda
   Hal itu jelas akan membuat makanan atau setidaknya sisa makanan dari mulut anda akan menetap di dalam harmonika
2. Jangan minum minuman yang lengket, atau pun minuman berat sebelum bermain
3. Akan lebih baik jika berkumur-kumur atau bahkan menyikat gigi jika perlu, sebelum bermain harmonika
4. Tempatkan/letakkan harmonika Anda di dalam kotaknya atau di tempat bersih lainnya disaat tidak dimainkan
5. Dikarenakan ukuran harmonika yang kecil, jadi perhatikan bahwa jangan meletakkanya sembarangan, sehingga bisa saja terduduki, terinjak, atau malah lupaanda lupa meletakkannya dimana.
6. Usahakan untuk menghadapkan bagian bawah harmonika kebawah setelah dimainkan. Hal ini bisa membantu mengeluarkan air liur yang mungkin ada didalam harmonika disaat kita memainkan sebelumnya.
7. Jangan pernah membiarkan orang lain memainkan harmonika anda.
   Yach..kecuali itu adalah seseorang yang tidak berkeberatan (dan tentunya anda tidak keberatan) untuk memainkan harmonika anda. mengingat disaat memainkannya kita pasti “mencium” harmonikanya…. dan terakhir
8. Pastikan anda menempatkan harmonika suatu tempat di yang nyaman dan sedekat mungkin dengan anda, jadi anda bisa memainkannya sesering mungkin.

Ada juga beberapa tips yang mungkin bisa sahabat #harmonicalovers terapkan ketika harmonica kalian dalam kondisi kotor pada bagian dalam harmonica:

1.  Ambil obeng dengan ukuran kecil sesuai dengan ukuran mur pada bagian samping harmonica kalian

2.  Buka penutup harmonica-nya setelah mur dan baut pada bagian samping harmonica terlepas

3.  Kemudian, ambil sehelai atau lebih tisu untuk membersihkan debu-debu yang menempel pada bagian reed harmonica (harap diperhatikan, kalian harus hati-hati ketika membersihkan reed harmonica karena jika sedikit saja reednya rusak bisa mempengaruhi suara harmonikanya)

4.  Bersihkan harmonica kalian dengan air (sebenarnya masih banyak yg bingung boleh tidak dibasuh dg air, takutnya nanti korosi dan mempengaruhi suara harmonikanya), namun jika kita rajin merawatnya sebenarnya tidak masalah kok, dan akan lebih bersih jika dibasuh dengan air. Setelah itu bersihkan dengan tissue.

5.  Kemudian, pasang lagi plat atau bagian penutup harmonica kalian.

6.  Harmonica kalian terlihat seperti harmonica baru lagi :)

Dikutip dari berbagai sumber

Gambar di atas diambil dari grup facebook pencinta harmonika

d overdraws